Introduction
This project deals with warping images in order to create image mosaics. After taking more than one photo of something, with a slight rotation in each photo, we can create an image mosaic by computing their Homographies from correspondence points, and then warping them and blending them.
Shoot the Pictures
When taking pictures, it is important to fix the center of projection so that the pixels correspond to roughly the same rays of light and the geometry concerning homographies is accurate. In order to accomplish this, I held my phone in such a way that turning it was about the vertical line through the middle of my lens. This approach led to pictures that look like the following.



Recover Homographies
From here, one can manually label correspondence points between each image. Though only four perfect correspondence points is required in theory, more points yields better results as there may be error in (1) the rotation of the camera about the center of projection and (2) the labeling of correspondence points. Thus, I made sure to label more than 4 points, spread roughly uniformly throughout the image. Below, the manually labeled correspondence points for the above example images are shown, with lines drawn between each correspondence point.


From here, we can simply use the formula presented in lecture (shown below) to compute the homographies from either image to either image, noting that we can set the scale factor i to be equal to 1. This shows why we would only theoretically need 4 points, as there are 8 unkowns.
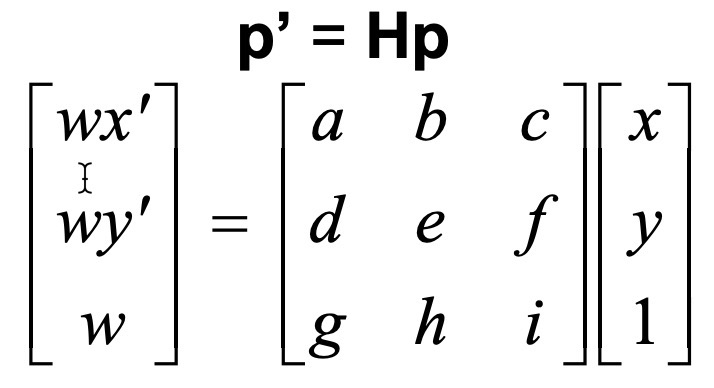
Warp the Images
Now we can compute the homographies from each image to the other image. This allows us to see what im1 would look like in the perspective of im2 and vice versa.



Image Rectification
Now that we can compute homographies and warp images, we have all of the tools necessary to rectify images. In order to do this,
we can take a picture of something we know has a rectangular shape. Then, we can choose a rectangular shape we want the object to
fit into. Next, we compute the corresponding homography and use it to warp the image, rectifying it.
Some examples are shown below.



Note that for some rectifications, this can lead to extreme warpings on the rest of the image, as seen in the last example with the happy face.
Blend the images into a mosaic
Now, we return to the original goal, creating an image mosaic. In order to do this, we must (1) warp the images to a common
perspective, (2) align the images based on some anchor points, and (3) blend the images to reduce artifacts. We have already
solved (1), so all that remains is to align the images based on anchor points and to perform blending.
First, we find an anchor point. Originally, I chose the average of all of the correspondences as my anchor point. However, this
led to the images ending up unaligned. This is because the average point is a linear combination of all of the points, but homographies
are not purely linear, so the average of each image's correspondence points might not correspond to each other. Thus, I chose an
anchor point by arbitrarily selecting corresponding correspondence points.
Then, we choose an image to fix and an image to warp. For the warped image, we compute its warped anchor point, which we use to align
to the image that we leave unwarped. From here, we can naively generate image mosaics, ignoring the blending step (3) for now. The
following are some examples of this process so far:


Clearly, this produces some pretty heavy artifacts, thus blending is required to produce quality image mosaics. In order to do blending, we use the procedure done in project 2, with Gaussian and Laplacian pyramids. This significantly improves the results, as shown below:





Note that for some of the mosaics above (the soccer field and messy room), multiple images are stitched to one base image. This is done by repeating the anchor point process multiple for times (once per image attached to the main image).
Detecting Harris interest points
Next, we want to manually identify correspondence points in order to fully automate the image stitching process. We roughly
follow the process described in “Multi-Image Matching using Multi-Scale Oriented Patches” by Brown et al.
First, we identify potential candidates by using Harris corner detection. The following showcases the strongest 2000 candidates
(excluding everything on the border) for each example image shown.


Adaptive Non-Maximal Suppression (ANMS)
Since we want the distribution of our points to end up being roughly uniform (to ensure stable homographies), we employ a technique known as Adaptive Non-Maximal Suppression (ANMS) on the detected Harris corner interest points. For each point, calculate a suppression radius according to the following:
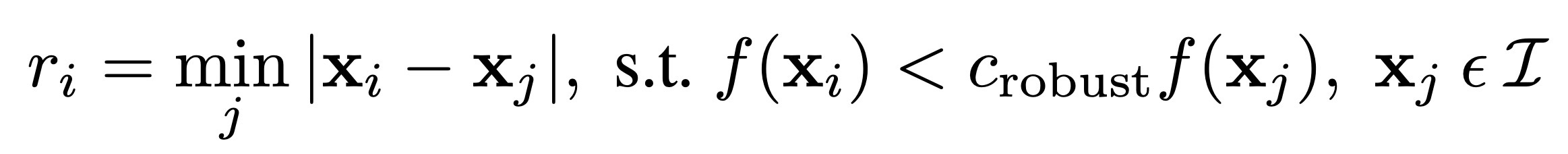
To get N interest points, we choose the N interest points with the largest suppression radii. Doing this process yields the following distribution of points.



Extracting feature descriptors
Now that we have a nice spread of interest points, we need to start matching them with other images. In order to do this, we extract a feature descriptor from each point. This takes the form of an 8x8 patch downsampled from the 40x40 window around the point, and normalized to have mean 0, variance 1. Some examples of extracted feature descriptors are shown below.
Feature matching
In order to perform feature matching, we compare the euclidean distance between every feature descriptor with every other
feature descriptor. We accept the point corresponding to the closest feature descriptor if the ratio between the closest
distance and second-closest distance is less than some threshold (0.4). This is to ensure that the best match is the best
match by a decent amount (the idea being that if there are multiple suitable matches, likely both are wrong since there
should only be one suitable match).
The results of running this feature matching process on the ANMS points is shown below, with corresponding points being
labeled the same color.



4-point RANSAC
Now that we have a small set of candidate points, we can run 4-point RANSAC on these points to find a robust homography.
4-point RANSAC (Random sample consensus) is an algorithm where we randomly sample four points, compute the resulting
homography, and count the number of inliers. We then choose the set with the most inliers and compute a homography from
that set. We define an inlier as a point that is sufficiently close to its corresponding point after being warped. This process
narrows down the set of matched features even more as it rejects most outliers and gives us a homography from points
that it has already checked will end up close to their corresponding points after being warped.
The following shows the resulting corresponding points after running 4-point RANSAC.



Putting it all together
We now have all of the tools to perform fully automatic image stitching. The following mosaics were made from 2, 3, or 4 images, and were created without any human input besides the capturing of the images. The correspondence points used to generate the homographies were fully automatically generated and the stitching and blending process were also fully automated.







What I learned
This project was the culmination of a variety of topics covered so far, and reinforced my understanding in
each part of the process of creating image mosaics. Of the many cool techniques used, I am most fond of the
ANMS technique for generating a more uniform distribution of points. I also found RANSAC very interesting as
a way to robustify the homographies. Utilizing random sampling to check for outliers is an idea that seems
applicable to many other domains.